

公開日:2021年11月22日午前4時47分 GMT
著作者 Sam Baron

多くの人は、数学は 人間の発明 だと考えています。この考え方では、数学は言語のようなものです。数学は世界の現実を記述するかもしれませんが、それを使用する人々の心の外に「存在する」わけではありません。
しかし、古代ギリシャのピタゴラス学派 (the Pythagorean school of thought) は異なる見解を持っていました。その支持者は、現実は根本的に数学的であると信じていました。
2,000年以上経った今、哲学者や物理学者はこの考えを真剣に受け止め始めています。
私が 新しい論文 で主張しているように、数学は物理的な世界に構造を与える自然の不可欠な要素です。
ミツバチと六角形
巣箱にいるミツバチは六角形の蜂の巣 (hexagonal honeycomb) を作ります。なぜでしょうか?
数学の「蜂の巣予想: honeycomb conjecture」によると、六角形は平面をタイル張りするのに最も効率的な形状です。均一な形状とサイズのタイルで表面を完全に覆い、周囲の長さを最小限にしたい場合は、六角形を使用するのがよいでしょう。
picture: The hexagonal pattern of honeycomb is the most efficient way to cover a space in identical tiles. Sam Baron, Author provided
ハニカムの六角形パターンは、同一のタイルで空間を覆う最も効率的な方法です。サム・バロン、著作者提供

チャールズ・ダーウィンは、蜂がこの形状を使用するように進化したのは、蜜ろうを生成するためのエネルギー入力を最小限に抑えながら、蜂蜜を貯蔵するための最大の巣を作るためだと 推論しました。
蜂の巣予想は古代に最初に提案されましたが、数学者トーマス・ヘイルズによって 1999 年に初めて 証明されました。
セミと素数
別の例を挙げましょう。北米の周期セミには、その生涯のほとんどを地中で過ごす 2 つの亜種があります。その後、13 年または 17 年ごとに (亜種によって異なります)、セミは 2 週間ほど 大群で 出現します。
なぜ 13 年と 17 年なのでしょうか。なぜ 12 年と 14 年ではないのでしょうか。あるいは 16 年と 18 年ではないのでしょうか。
1 つの説明 は、13 と 17 が素数 (prime number) であるという事実に訴えるものです。

セミ (cicada) には、彼らと同様に人生の大半を地中で過ごすさまざまな捕食者がいると想像してください。セミは、捕食者が休眠しているときに地中から出てくる必要があります。
2、3、4、5、6、7、8、9 年のライフサイクルを持つ捕食者がいるとします。これらすべてを回避する最善の方法は何でしょうか?
では、13 年のライフサイクルと 12 年のライフサイクルを比較してみましょう。 12 年のライフサイクルを持つセミが地中から出てくると、2 年、3 年、4 年の捕食者も地中から出てきます。2、3、4 はすべて 12 に均等に分割されるからです。
13 年のライフサイクルを持つセミが地中から出てくると、その捕食者は誰も地中から出てきません。2、3、4、5、6、7、8、9 のどれも 13 に均等に分割されないからです。17 についても同じことが言えます。
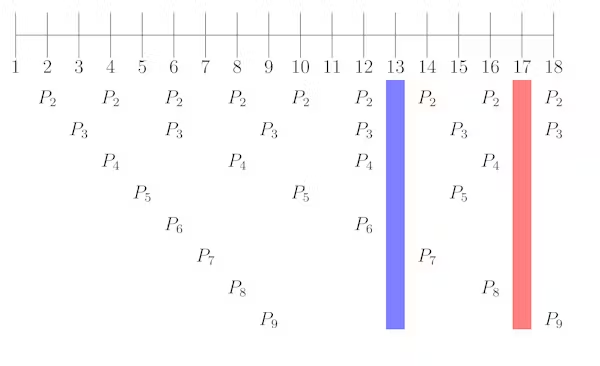
これらのセミは、数字に関する基本的な事実を利用するように 進化したよう です。
創造か発見か?
探し始めると、他の例を見つけるのは簡単です。石鹸の膜 の形から、エンジンの ギア設計、土星の環の隙間の位置と大きさまで、数学はいたるところに存在します。
数学が私たちの周りで目にする多くのことを説明できるのであれば、数学は私たちが作り出したものである可能性は低いでしょう。あるいは、数学的事実は人間だけでなく、昆虫、シャボン玉、燃焼エンジン、惑星によって発見されるということもあります。
プラトンはどう考えていたのでしょうか。
しかし、私たちが何かを発見しているとしたら、それは何なのでしょうか。
古代ギリシャの哲学者プラトン (Plato) には答えがありました。彼は、数学は実際に存在する物体を説明するものだと考えていました。
プラトンにとって、これらの物体には数字 (numbers) や幾何学的形状 (geometric shape) が含まれていました。今日では、グループ、カテゴリ、関数、フィールド、リングなどのより複雑な数学的物体 (mathematical objects) をリストに加えるかもしれません。

プラトンはまた、数学的物体は空間と時間の外側に存在すると主張しました。しかし、そのような見方は、数学がどのように何かを説明するのかという謎を深めるだけです。
説明には、世界にあるものが他のものにどのように依存しているかを示すことが含まれます。数学的物体が私たちの住む世界とは別の領域に存在する場合、それらは物理的なものと関係することはできないようです。
ピタゴラス学派の登場
古代ピタゴラス学派は、数学は物体の世界を記述するという点でプラトンに同意しました。しかし、プラトンとは異なり、彼らは数学的物体が空間と時間を超えて存在するとは考えませんでした。
その代わりに、彼らは物質 (matter) が原子 (atoms) でできているのと同じように、物理的現実は数学的対象でできていると信じていました。
現実が数学的対象でできているなら、数学が私たちの周りの世界を説明する上でどのような役割を果たすかは容易に理解できます。

過去 10 年間で、2 人の物理学者がピタゴラスの立場を強力に擁護してきました。スウェーデン系米国人の宇宙学者マックス・テグマーク: Max Tegmark とオーストラリアの物理学者で哲学者のジェーン・マクドネル: Jane McDonnell です。
テグマークは、現実 (reality) は 1 つの大きな数学的対象にすぎないと主張しています。それが奇妙に思えるなら、現実はシミュレーション (simulation) であるという考えについて考えてみてください。シミュレーションはコンピューター プログラムであり、数学的対象の一種です。
マクドネルの見解はより過激です。彼女は、現実は数学的対象と心 (minds) でできていると考えています。数学は、意識を持つ宇宙が自分自身を知る方法です。
私は 別の見解 を擁護しています。世界には数学 (mathematics) と物質 (matter) の 2 つの部分があります。数学は物質に形 (form) を与え、物質は数学に実体 (substance) を与えます。
数学的対象は、物理世界の構造的枠組みを提供します。
数学の未来
物理学でピタゴラス主義が再発見されているのは理にかなっています。
過去 1 世紀、物理学はますます数学的になり、物理世界を説明するために、群論 (group theory) や微分幾何学 (differential geometry) などの一見抽象的な研究分野に目を向けるようになりました。
物理学と数学の境界があいまいになるにつれて、世界のどの部分が物理的で、どの部分が数学的であるかを判断することが難しくなっています。
しかし、ピタゴラス学派が哲学者によって長い間無視されてきたのは奇妙です。
私はそれが変わりつつあると信じています。ピタゴラス学派の革命の時が来たのです。それは現実に対する私たちの理解を根本的に変えることを約束する革命です。

この記事は、クリエイティブコモンズライセンス(CCL)の下で The Conversation と各著作者からの承認に基づき再発行されています。日本語訳は archive4ones(Koichi Ikenoue) の翻訳責任で行われています。オリジナルの記事を読めます。original article.


